Contoh Soal Pertidaksamaan Irasional Lengkap dengan Pembahasan

14.6K

Hai Quipperian, di artikel sebelumnya, Quipper Blog sudah pernah membahas tentang pertidaksamaan irasional beserta tips untuk menyelesaikan soalnya. Apakah kamu masih ingat bagaimana caranya? Agar kamu tidak lupa, kali ini Quipper Blog akan membahas beberapa contoh soal terkait pertidaksamaan irasional. Ingin tahu selengkapnya? Yuk, check this out!

Contoh soal 1

Himpunan penyelesaian dari pertidaksamaan 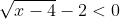adalah

1. {x| 4 ≤ x < 8}
2. {x| 2 < x < 8}
3. {x| 4 ≤ x < 12}
4. {x| 0 ≤ x < 8}
5. {x| 1 ≤ x < 4}

Pembahasan:

Bentuk pertidaksamaan pada soal mengikuti bentuk adalah

Pertidaksamaan tersebut harus memenuhi syarat berikut.

1. f ≥ (X) 0
   x – 4 ≥ 0
   x ≥ 4
2. f(x) < 2 ²
   x-4 < 2 ²
   x < 8

Himpunan penyelesaian dari pertidaksamaan tersebut merupakan irisan dari poin (a) dan (b) yang dinyatakan dalam bentuk garis bilangan berikut.

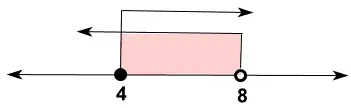
Jadi, himpunan penyelesaian pertidaksamaan 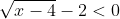adalah {x| 4 ≤ x < 8}

Jawaban: A

Contoh soal 2

Himpunan penyelesaian dari pertidaksamaan 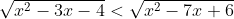adalah …

1. { 0 < x ≤ -1}
2. {x ≤ -1}
3. {x ≤ 1}
4. {-2 < x ≤ -1}
5. {x ≥ -1}

Pembahasan:

Diketahui:

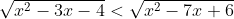
Bentuk pertidaksamaan di atas mengikuti bentuk

Oleh sebab itu, pertidaksamaan tersebut harus memenuhi syarat berikut ini.

1. f(x) ≥ 0
   x² – 3x – 4 ≥ 0
   (x-4)(x+1) ≥ 0
   x ≥ 4 atau x ≤ – 1
2. f(x) ≥ 0
   x² – 7x + 6 ≥ 0
   (x-6)(x-1) ≥ 0
   x ≥ 6 atau x ≤ 1
3. f(x) < g (x)
   x² – 3x – 4 < x² – 7x + 6
   4x < 10
   x < 5/2

Penyelesaian pertidaksamaan irasional tersebut merupakan irisan dari ketiga penyelesaian, yaitu (a), (b), dan (c) seperti pada garis bilangan berikut.

Jadi, himpunan penyelesaiannya adalah {x ≤ -1}.

Jawaban: B

Contoh soal 3

Himpunan penyelesaian dari pertidaksamaan 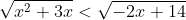adalah

1. {x| -7 < x < -3} atau {x| 0 < x < 2}
2. Hanya {x| – 7 < x < -3}
3. Hanya {x| 0 < x < 2}
4. {x| -3 < x < 0} atau {x| 0 < x < 2}
5. {x| -7 < x < 0} dan {x| 0 < x < 7}

Pembahasan:

Pertidaksamaan tersebut memenuhi bentuk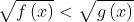

Agar bisa ditentukan himpunan penyelesaiannya, pertidaksamaan tersebut harus memenuhi syarat-syarat berikut.

1. f(x) ≥ 0
   x² + 3x ≥ 0
   x (x+3) ≥ 0
   x ≥ 0 atau ≤ -3
2. g(x) ≥ 0
   -2x + 14 ≥ 0
   -2x ≥ -14
   x ≤ 7
3. f(x) < g(x)
   x² + 3x < -2x + 14
   x² + 3x + 2x – 14 < 0
   x² + 5x – 14 < 0
   (x-2)(x+7) < 0
   -7 < x < 2

Himpunan penyelesaiannya merupakan irisan dari poin a, b, dan c yang diperoleh dari garis bilangan berikut.

Berdasarkan garis bilangan di atas, terdapat dua solusi yang memenuhi (diarsir warna hijau), yaitu sebagai berikut.

• {x| – 7 < x < -3}
• {x| 0 < x < 2}

Jadi, himpunan penyelesaian pertidaksamaan pada soal adalah {x| – 7 < x < -3} atau {x| 0 < x < 2}.

Jawaban: A

Contoh soal 4

Himpunan penyelesaian dari pertidaksamaan adalah….

1. {-5, -6}
2. {4, 5, 6}
3. {1, 2, 3}
4. {-1, -2}
5. {5, 6}

Dengan demikian, bentuk pertidaksamaan tersebut harus memenuhi ketentuan berikut ini.

1. f(x) ≥ 0
   x+2 ≥ 0
   x ≥ -2
2. g(x) > 0
   x-4 > 0
   x > 4
3. f(x) > g² (x)
   x+2 > (x – 4)²
   x+2 > x² 8x+16
   -x² + 9x – 14 > 0
   (-x + 7)(x-2) > 0
   2 < x < 7

Himpunan penyelesaian diperoleh dari irisan pada poin a, b, dan c seperti pada garis bilangan berikut.

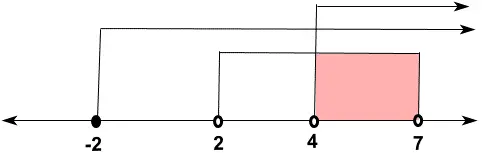
Jadi, himpunan penyelesaian dari pertidaksamaan adalah {5, 6}

Jawaban: E

Contoh soal 5

Nilai x yang memenuhi pertidaksamaan adalah…

1. {1, 2, 3, 4, 5, …}
2. {-1, -2, -3, -4, -5, …}
3. {2, 3, 4, 5, 6, …}
4. {0, 1, 2, 3, 4, …}
5. {-2, -3, -4, -5, …}

Pembahasan:

Pertidaksamaan pada soal merupakan bentuk dari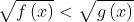

Oleh sebab itu, pertidaksamaan tersebut harus memenuhi tiga syarat seperti berikut.

1. f(x) ≥ 0
   x² + x – 2 ≥ 0
   (x+2)(x-1) ≥ 0
   x ≤ -2 atau x ≥ 1
2. g(x) > 0
   x+1 > 0
   x > -1
3. f²(x) < g²(x)
   x² + x -2 < (x+1)²
   x² + x -2 < x² + 2x + 1
   -3x – 3 < 0
   -3x < 3
   x > -1

Nilai x yang memenuhi merupakan irisan dari poin a, b, dan c seperti ditunjukkan oleh garis bilangan berikut.

Jadi, nilai x yang memenuhi adalah {x|x > 1}, yaitu {2, 3, 4, 5, 6, …}.

Jawaban: C

Contoh soal 6

Seorang atlet, melempar lembing hingga tepat mengenai titik yang telah ditentukan. Waktu yang diperlukan lembing untuk sampai ke titik sasaran dinyatakan sebagai t

dengan persamaan lintasan x(t) = dengan x dalam meter. Agar tidak didiskualifikasi, panjang lintasan minimal yang harus dilalui lembing adalah 5 m. nilai t yang memenuhi adalah

1. 0<t<8
2. t ≤ 0 atau t ≥ 8
3. t ≥ 0 atau t ≤ 8
4. t ≤ -1 atau t ≥ 8
5. t ≤ 0 atau t ≥ 6

Pembahasan:

Mula-mula, kamu harus menentukan bentuk umum masalah pertidaksamaan pada soal.

Di soal diketahui bahwa persamaan lintasan lembing dan panjang lintasan minimalnya 5 m. Secara matematis, hubungan keduanya dinyatakan sebagai berikut.

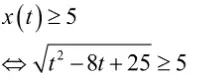
Selanjutnya, tentukan diskriminan dari x(t). Diskriminan ini digunakan untuk mengetahui jenis definit.

Nilai diskriminannya D < 0. Artinya, bentuk persamaan kuadrat tersebut merupakan definit positif, sehingga akan selalu terpenuhi.

Terakhir, kamu bisa menentukan nilai t dengan cara berikut.

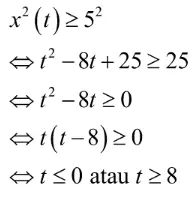
Jadi, nilai t yang memenuhi adalah t ≤ 0 atau t ≥ 8

Jawaban: B

Sampai sini, apakah Quipperian sudah paham? Itulah pembahasan Quipper Blog kali ini tentang contoh soal pertidaksamaan irasional.