Contoh Soal Pertidaksamaan Kuadrat Lengkap dengan Pembahasan

57.2K

Hai Quipperian, apakah kamu masih ingat konsep pertidaksamaan kuadrat? Di artikel sebelumnya, Quipper Blog pernah membahas tentang pertidaksamaan kuadrat lengkap dengan penjabaran garis bilangannya. Nah, pada artikel ini kamu akan diajak untuk menyimak contoh soal tentang pertidaksamaan kuadrat, lho. Daripada penasaran, yuk cekidot!

Contoh Soal 1

Suatu pertidaksamaan kuadrat menghasilkan garis bilangan seperti berikut.

Solusi yang tepat untuk pertidaksamaan kuadrat tersebut adalah

1. {x|-2 < x ≤ 3}
2. x|x ≤ -2 atau x ≥ 3}
3. {x|x ≥ -2 atau x ≤3}
4. {x|x <2 atau x > 3}
5. {x|x ≤ -2 atau x < 3}

Pembahasan:

Garis bilangan pada soal memiliki dua titik utama, yaitu – 2 dan 3. Titik utama itu berupa bulatan penuh. Artinya, bilangan yang berada di titik tersebut termasuk sebagai solusi. Dengan demikian, solusi yang tepat adalah {x| x ≤ -2 atau x ≥ 3}.

Jawaban: B

Contoh Soal 2

Himpunan penyelesaian dari pertidaksamaan x² – 3x – 4 < 0 adalah

1. {x| -1 < x < 4}
2. {x| 1< x < 4}
3. {x| -4 < x < 1}
4. {x| x < 1 atau x > 4}
5. {x| -3 < x < 4}

Pembahasan:

Mula-mula, kamu harus memfaktorkan bentuk kuadrat yang berada di ruas kiri seperti berikut.

x2 – 3x – 4 <

⇔ (x – 4) ( x + 1) < 0

Selanjutnya, tentukan titik pembuat nolnya.

(x – 4) ( x + 1) < 0

⇔ x = 4 atau x = -1

Substitusikan titik pembuat nol pada garis bilangan.

Jadi, himpunan penyelesaiannya adalah {x|-1 < x < 4}.

Jawaban: A

Contoh Soal 3

Himpunan penyelesaian dari pertidaksamaan 2x² – x + 1 > 0 adalah

1. {x| x < 1 atau x > 3/2}
2. {x| -1 < x < 3/2}
3. {x| x < -1 atau x > 3/2}
4. {x| x > -1 atau x < 3/2
5. {x| x < -1 atau x ≥ 3/2}

Pembahasan:

Mula-mula, kamu harus memfaktorkan bentuk kuadrat pada soal.

2x² – x + 1 > 0

⇔ (2x – 3) ( x + 1) > 0

Selanjutnya, tentukan titik pembuat nolnya.

Substitusikan nilai x pembuat nolnya pada garis bilangan.

Jadi, himpunan penyelesaian pertidaksamaan tersebut adalah {x| x < -1 atau x > 3/2}

Jawaban: C

Contoh Soal 4

Nilai x yang memenuhi pertidaksamaan x² – 2x ≥ 24 adalah

1. x < -4 atau x ≥ 6
2. x > -4 atau x <6
3. x ≤ -2 atau x ≥ 6
4. x ≤ -6 atau x ≥ 4
5. x ≤ -4 atau x ≥ 6

Pembahasan:

Pertama, kamu harus mengubah sistem pertidaksamaan pada soal menjadi sistem pertidaksamaan kuadrat. Lalu, lakukan pemfaktoran.

x² – 2x ≥ 24

⇔ x² – 2x – 24 ≥ 0

⇔ (x – 6) (x+4) ≥ 0

Selanjutnya, tentukan titik pembuat nolnya.

(x – 6)(x+4) = 0

⇔ x = 6 atau x = -4

Substitusikan nilai x pembuat nol pada garis bilangan. Ingat, tanda pertidaksamaannya adalah lebih besar sama dengan. Artinya, titik bulatannya harus penuh, ya.

Jadi, nilai x yang memenuhi adalah x ≤ -4 atau x ≥ 6.

Jawaban: E

Contoh Soal 5

Solusi dari pertidaksamaan x² – 5x – 14 ≤ 0 adalah

1. {x|x <-2 atau x>7}
2. {x|-7
3. {x|2
4. {x|-2≤x≤7}
5. {x|-1

Pembahasan:

Pertama, kamu harus memfaktorkan bentuk kuadrat pada soal.

x2 – 5x – 14 ≤ 0

(x – 7)(x – 2) ≤ 0

Selanjutnya, tentukan titik pembuat nolnya.

(x – 7)(x – 2) ≤ 0

⇔ x = 7 atau x = -2

Substitusikan nilai x pembuat nol pada garis bilangan. Ingat, tanda pertidaksamaannya adalah lebih besar sama dengan. Artinya, titik bulatannya harus penuh, ya.

Jadi, solusi dari pertidaksamaan tersebut adalah {x|-2≤x≤7}.

Jawaban: D

Contoh Soal 6

Diketahui pertidaksamaan kuadrat seperti berikut.

x² – x + 2 ≤ – x² + x + 6

Nilai x yang memenuhi sistem pertidaksamaan tersebut adalah

1. {-1, 0, 1, 2}
2. {0, 1}
3. {-2, -1, 0, 1}
4. {1, 2, 3, 4}
5. {2, 3}

Pembahasan:

Mula-mula, ubahlah bentuk pertidaksamaan tersebut menjadi bentuk pertidaksamaan kuadrat. Lalu, lakukan pemfaktoran.

x2 – x + 2 ≤ – x2 + x + 6

⇔ x² – x + 2 + x² – x – 6 ≤ 0

⇔ 2x² – 2x – 4 ≤ 0

⇔ x² – x – 2 ≤ 0

⇔ (x – 2)(x + 1) ≤ 0

Tentukan titik pembuat nolnya.

(x – 2)(x + 1) ≤ 0

⇔ x = 2 atau x = -1

Substitusikan nilai x pembuat nol pada garis bilangan.

Jadi, nilai x yang memenuhi adalah {-1, 0, 1, 2}.

Jawaban: A

Contoh Soal 7

Perhatikan pertidaksamaan kuadrat berikut.

x² – 9x + 14 ≥ 22

Nilai x yang termasuk solusi dari pertidaksamaan tersebut adalah

1. 10
2. 7
3. 5
4. 6
5. 4

Pembahasan:

Mula-mula, ubahlah bentuk pertidaksamaan pada soal menjadi pertidaksamaan kuadrat seperti berikut.

x2 – 9x + 14 ≥ 22

⇔ x² – 9x + 8 ≥ 0

Lakukan pemfaktoran bentuk pertidaksamaan di atas.

x² – 9x + 8 ≥ 0

⇔ (x – 8)(x – 1) ≥ 0

Tentukan titik pembuat nolnya.

(x – 8)(x – 1) ≥ 0

⇔ x = 8 atau x = 1

Substitusikan nilai x tersebut ke garis bilangan.

Nilai x yang memenuhi adalah x ≤ 1 atau x ≥ 8

Jadi, nilai x yang termasuk solusi adalah 10

Jawaban: A

Contoh Soal 8

Tingkat reproduksi buaya di sebuah pusat penangkaran mengikuti persamaan berikut.

dengan t dalam tahun

Waktu yang diperlukan untuk menghasilkan paling sedikit 9 buaya adalah

1. Minimal 6 bulan
2. Minimal 2,5 tahun
3. Minimal 1 tahun
4. Minimal 2 tahun
5. Minimal 1,5 tahun

Pembahasan:

Di soal ditanyakan waktu yang dibutuhkan untuk menghasilkan paling sedikit 9 ekor buaya.

Secara matematis, bisa dinyatakan sebagai f (t) ≥ 9. Oleh karena terdapat keterangan “paling sedikit”, maka persamaan kuadrat tersebut harus dijadikan pertidaksamaan.

f (t) ≥ 9

⇔ 2t² + 3t + 4 ≥ 9

⇔ 2t² + 3t – 5 ≥ 0

Lalu, lakukan pemfaktoran untuk mencari titik pembuat nolnya.

2t² + 3t – 5 ≥ 0

⇔ (2t + 5)(t – 1) ≥ 0

⇔ (2t + 5)(t – 1) = 0

⇔ t = -5/2 = -2,5 atau 1 = 1

Substitusikan nilai t pembuat nol pada garis bilangan.

Garis bilangan di atas memuat dua buah solusi, yaitu t ≤ -2,5 atau t ≥ 1. Oleh karena waktu tidak ada yang bernilai negatif, maka nilai t yang memenuhi adalah t ≥1.

Jadi, waktu yang diperlukan untuk menghasilkan paling sedikit 9 ekor buaya adalah minimal 1 tahun.

Jawaban: C

Contoh Soal 9

Bu Rumini memiliki usaha pengolahan sambal kemasan. Hasil produksi sambal Bu Rumini, mengikuti persamaan berikut.

p(x) = x² – 35x + 400

Dengan p(x) merupakan banyaknya hasil produksi sambal (botol) dan x merupakan massa cabai dalam kg.

Jika Bu Rumini ingin memproduksi maksimal 100 botol sambal, cabai yang harus disediakan adalah

1. 10 sampai 15 kg
2. 20 sampai 25 kg
3. 17 sampai 30 kg
4. 15 sampai 20 kg
5. Lebih dari 30 kg

Pembahasan:

Oleh karena besaran yang diminta adalah jumlah produksi maksimal 100 botol, maka persamaan produksi sambal Bu Rumini harus kamu jadikan pertidaksamaan seperti berikut.

p(x) ≤ 100

⇔ x² – 35x + 400 ≤ 100

⇔ x² – 35x + 300 ≤ 0

Lakukan pemfaktoran untuk mencari titik pembuat nolnya.

x2 – 35x + 300 ≤ 0

⇔ (x – 20)(x – 15) = 0

⇔ x = 20 atau x = 15

Jadi, cabai yang harus disediakan adalah 15 sampai 20 kg.

Jawaban: D

Contoh Soal 10

Sebuah bangun persegi panjang memiliki panjang (x + 5) cm dan lebar (x – 1) cm. Jika luas bangun tersebut tidak boleh lebih dari 40 cm2, nilai x yang memenuhi adalah

1. {-9 ≤ x ≤ 5}
2. {x ≥ 5}
3. 2, 3, 4, 5
4. {x ≤ 5}
5. {1, 2, 3}

Pembahasan:

Persegipanjang memiliki panjang (x + 5) cm dan lebar (x – 1) cm dan luasnya tidak boleh lebih dari 40 cm2. Untuk mencari nilai x, ubahlah keterangan tersebut ke dalam bentuk prtidaksamaan.

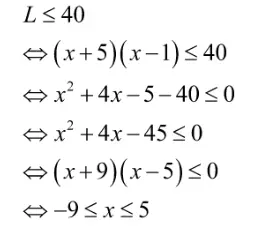
Himpunan penyelesaiannya {-9, -8, -7, …, 5}

Oleh karena panjang dan lebar tidak mungkin negatif, maka nilai x yang memenuhi adalah {2, 3, 4, dan 5}.

Jadi, nilai x yang memenuhi adalah {2, 3, 4, 5}.

Jawaban: C

Setelah melihat 10 contoh soal di atas, apakah Quipperian sudah paham bagaimana cara menyelesaikan soal-soal pertidaksamaan kuadrat?