Hai Quipperian, bagaimana kabarnya? Semoga selalu sehat dan tetap semangat belajar Matematika, ya!
Martina menjatuhkan bola bekel dari atas meja setinggi 80 cm. Jelas bahwa bola bekel akan memantul sampai akhirnya berhenti. Pantulan bola pertama pasti lebih tinggi dari pantulan kedua, pantulan kedua lebih tinggi dari pantulan ketiga, dan seterusnya.
Setelah diamati, ternyata setiap kali bola memantul, tingginya menjadi 1/2 kali dari tinggi pantulan sebelumnya. Martina semakin penasaran, kira-kira berapa panjang lintasan bola dari awal memantul sampai berhenti? Apakah kamu ingin membantu Martina? Bagaimana caranya?
Ternyata, Martina bisa menghitung panjang lintasan bola menggunakan deret geometri tak hingga, lho. Ayo segera bantu Martina menghitung panjang lintasan bola bersama Quipper Blog.
Pengertian Deret Geometri Tak Hingga

Sebelum membantu Martina, kamu harus tahu dulu apa itu deret geometri tak hingga.
Deret geometri tak hingga adalah penjumlahan suku-suku pada barisan geometri yang banyaknya tidak terbatas (tak hingga). Deret geometri tak hingga biasanya dinotasikan sebagai S∞. Secara matematis, deret geometri tak hingga dirumuskan sebagai berikut.
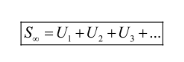
Jenis-jenis Deret Geometri Tak Hingga

Secara umum, deret geometri dibagi menjadi dua jenis, yaitu deret geometri tak hingga yang konvergen dan divergen.
1. Deret geometri tak hingga konvergen
Konvergen artinya memusat atau tidak menyebar. Deret geometri tak hingga yang konvergen berarti deret geometri yang masih memiliki limit jumlah. Syarat deret geometri tak hingga jenis ini adalah rasio berada di antara -1 dan 1, yaitu -1 < r < 1 atau |r| < 1. Untuk jumlah tak hingganya dirumuskan sebagai berikut.

2. Deret geometri tak hingga divergen
Divergen artinya menyebar. Deret geometri tak hingga yang divergen berarti deret geometri tak hingga yang tidak terbatas jumlahnya. Syarat deret geometri tak hingga yang divergen adalah r < -1 atau r > 1. Untuk jumlah tak hingganya dirumuskan sebagai berikut.

Setelah mempelajari konsep dasar deret geometri tak hingga di atas, apakah kamu sudah siap untuk membantu Martina menghitung panjang lintasan bola bekelnya? Jika sudah siap, let’s go!
Ayo, Bantu Martina!

“Hmm, Martina ada-ada nih, kenapa juga dia harus menjatuhkan bola dari atas meja?” Eitss, jangan berpikir seperti itu ya. Siapa tahu dengan kamu membantu Martina, pemahamanmu tentang deret geometri tak hingga menjadi semakin baik. Daripada panjang lebar, coba kamu tentukan dulu, apa saja besaran yang diketahui.
Diketahui:
Tinggi meja Martina anggap sebagai a = 80 cm

Pembahasan:
Kira-kira, barisan yang dibentuk oleh pantulan bola bekel milik Martina termasuk konvergen atau divergen ya?
Untuk tahu, coba cek rasionya!
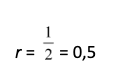
Rasio 0,5 merupakan syarat terbentuknya deret geometri tak hingga yang konvergen. Kamu juga harus ingat bahwa tertulis kata “berhenti”. Apakah artinya? Berhenti merupakan kondisi di mana bola tidak lagi memantul. Setelah bola berhenti, tentu tidak akan ada lagi lintasan yang akan terbentuk.
Pada kondisi semacam ini, kamu akan kesulitan untuk menentukan berapa kali bola akan memantul hingga akhirnya berhenti. Hal yang bisa kamu tentukan adalah panjang lintasan bola mulai awal jatuh menyentuh lantai sampai berhenti. Untuk itu, gunakan persamaan berikut.

Dengan:
a adalah tinggi pantulan awalnya, yaitu 80 cm;
r adalah rasio = 0,5.

Jika digambarkan menjadi seperti berikut.

Sebelum menghitung panjang lintasan bolanya, kamu harus tau bahwa setiap lintasan akan dilewati dua kali, kecuali lintasan awal.
80, 40, 40, 20, 20, 10, 10, …, …,
Dengan demikian, S∞ dibedakan menjadi S∞ suku ganjil dan genap. Suku ganjil dimulai dari a = 80 cm, sedangkan suku genap dimulai dari a = 40 cm.
Untuk suku ganjil
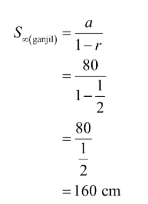
Untuk suku genap
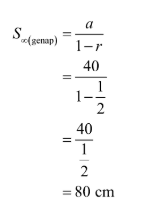
Total panjang lintasan bola bekel Martina
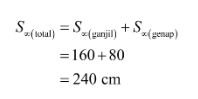
Jadi, panjang lintasan yang ditempuh bola bekel Martina adalah 240 cm.
Horee, akhirnya Martina sudah tahu berapa panjang lintasan yang ditempuh bola bekelnya mulai awal memantul sampai berhenti.
Tidak cukup sampai di situ, kamu harus mencoba menyelesaikan soal lain yang berkaitan dengan deret geometri tak hingga. Berikut contoh soalnya.
Contoh soal 1
Perhatikan gambar berikut.
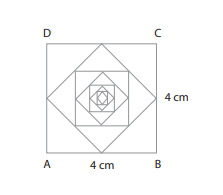
Di dalam persegi ABCD di atas, terdapat persegi-persegi lain secara terus menerus di mana 4 titik sudutnya diambil dari titik tengah persegi sebelumnya. Tentukan jumlah luas persegi yang terbentuk!
Pembahasan:
Perhatikan persegi yang pertama dan kedua berikut ini.

Nyatakan luas total sebagai L. Secara matematis, L dirumuskan sebagai berikut.

Tentukan luas persegi ABCD
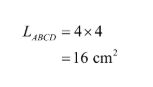
Luas total persegi
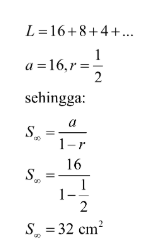
Jadi, luas persegi yang terbentuk adalah 32 cm2.
Contoh soal 2


Jadi, agar deretnya menjadi konvergen, syaratnya adalah x > 2 atau x < 0.
Itulah pembahasan tentang deret geometri. Kamu harus bangga karena sudah bisa membantu Martina menemukan panjang lintasan bola bekelnya. Jangan lupa untuk terus berlatih mengerjakan latihan soal, terlebih soal-soal yang sifatnya penerapan.
Untuk mendukung semua aktivitas belajarmu, Quipper Video hadir dengan berbagai fitur, mulai video penjelasan tutor, buku panduan, video animasi, sampai latihan soal beserta pembahasannya. Tunggu apa lagi, buruan gabung bersama Quipper Video. Salam Quipper!
[spoiler title=SUMBER]
- https://d14fikpiqfsi71.cloudfront.net/media/W1siZiIsIjIwMTUvMTEvMDYvMDYvNTgvMTUvOTE0MmFkNjgtMTZmNS00MmNkLWE3ZDktMzMzMGFjYjg4ZDFhL01hdGVtYXRpa2ElMjBTZXNpJTIwMTcucGRmIl1d.pdf?sha=3f7f4f58b1c5ec4d
- http://www.learn.quipper.com
- https://www.defantri.com/2017/02/menghitung-deret-geometri-tak-hingga.html%5B/spoiler%5D
Penulis: Eka Viandari
