Halo Quipperian! Pada sesi kali ini, Quipper Blog akan membahas suatu topik yang menarik lho buat kalian yaitu “ Mengenal Irisan Kerucut pada Parabola”. Sebagaimana kita ketahui bahwa Irisan Kerucut terdiri dari 3 jenis yaitu Hiperbola, Elips, dan Parabola. Tiga jenis Irisan kerucut tersebut memiliki karakteristik dan sifat-sifat yang beda.
Penting bagi Quipperian mengenali karakteristik dan sifat-sifat Irisan Kerucut parabola sehingga penggunaan rumus untuk penyelesaian tidak salah pakai dan mendapatkan hasil jawaban yang tepat. Oleh sebab itu, pada kesempatan kali ini, Quipper Blog akan membahas secara detail tentang:
- Definisi parabola dan elemen-elemen di dalamnya
- Kedudukan garis terhadap parabola dan persamaannya
- Persamaan garis singgung parabolanya
- Contoh soal dalam irisan kerucut parabola
- Contoh soal dan pembahasan dari bank soal Quipper tentang irisan kerucut pada parabola.
Yuk, kita mulai pembahasannya!
Definisi Parabola
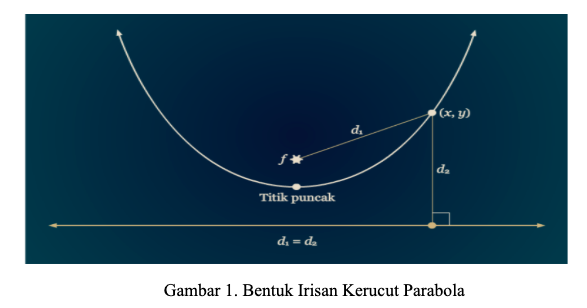
Dimisalkan terdapat suatu titik tertentu misalkan f dan garis tertentu misalkan D berada di dalam suatu bidang. Parabola adalah himpunan semua titik (x,y) sedemikian sehingga jarak antara f dan titik (x,y) sama dengan jarak antara D dan (x,y). Titik f ini disebut fokus parabola sedangkan garis D disebut sebagai direktriks. Bentuk parabola ditunjukkan pada gambar 1.
Suatu parabola memiliki suatu persamaan. Kita misalkan suatu parabola memiliki titik puncak di (0,0) dan memiliki titik fokus di (o,p). parabola tersebut memiliki nilai direktriks dengan persamaan y = -p, sehingga semua titik pada D dapat dituliskan sebagai (x,-p). parabola tersebut ditunjukkan pada gambar 2. Sehingga dengan menggunakan rumus jarak dan menerapkan definisi bahwa d1 = d2. Diperoleh persamaan parabolanya sebagai berikut:
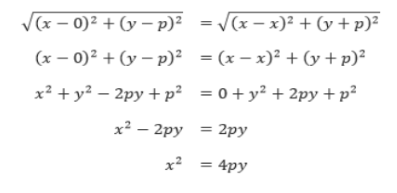
Persamaan di atas disebut persamaan bentuk fokus-direktriks dari suatu parabola vertikal dengan nilai puncak di (),0). Namun apabila parabola di atas diputar sehingga terbuka ke kanan, maka akan diperoleh suatu parabola horizontal dengan titik puncak di (0,0) dan nilai persamaanya adalah y2 = 4px.
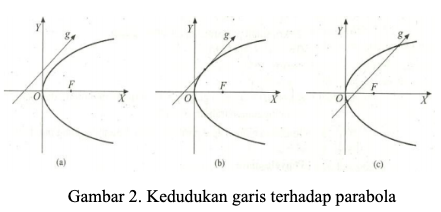
Setiap garis memiliki kedudukan terhadap suatu parabola. Kedudukan ini memiliki hubungan terhadap suatu diskriminan (D) terhadap parabolanya. Terdapat 3 jenis kedudukan terhadap parabola yaitu garis tidak memotong parabola, garis memotong 1 titik di parabola, dan garis memotong 2 titik di parabola. Gambar kedudukan garis terhadap parabola adalah sebagai berikut:
- → garis tidak memotong parabola
- → garis menyinggung (memotong 1 titik parabola)
- → garis memotong 2 titik parabola
Misalkan terdapat persamaan kuadrat baru pada parabola yaitu : ax2 + bx + c = 0 → D = b – 4.a.c dapat dinyatakan :
- D < 0 → garis tidak memotong parabola
- D = 0 → garis memotong 1 titik di parabola
- D > 0 → garis memotong 2 titik di parabola
Persamaan Garis Singgung Parabola
Garis singgung merupakan garis yang hanya memiliki satu titik persekutuan (titik singgung) dengan kurva. Dalam suatu parabola terdapat garis singgung titik singgung yang terletak pada parabola dan titik singgung yang terletak di luar parabola. Persamaan garis singgungnya adalah sebagai berikut :
- Parabola berpuncak di (0,0) :
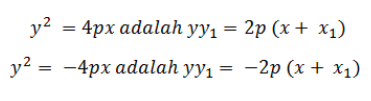
- Parabola berpuncak di (a,b)
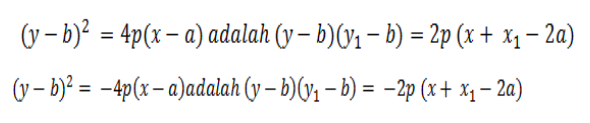
Persamaan Garis Singgung di Luar Parabola

Apabila sebuah titik P (x1 , y1) di luar parabola ditarik 2 buah garis singgung, maka garis penghubung p antara kedua titik singgungnya disebut garis polar p terhadap parabola dan P disebut titik polar garis p.
- Parabola berpuncak di (0,0)

- Parabola berpuncak di (a,b)
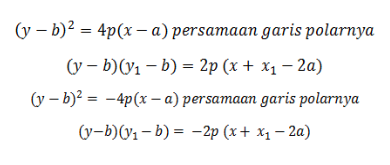
Persamaan garis singgung parabola dengan gradient tertentu (m) :
- Parabola berpuncak di (0,0) :
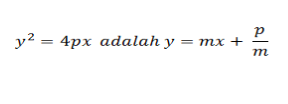
- Parabola berpuncak di (a,b) :

Sebagai Warming Up, untuk memahami konsep dan rumus-rumus di atas, Quipper Blog akan memberikan contoh soal dan pembahasannya, Let’s move it!!
Contoh soal: Kedudukan garis terhadap parabola
1. Tempat kedudukan garis y = x + 4 terhadap parabola y2 = 12x
Pembahasan:
Jika persamaan y = x + 4 disubtitusikan ke dalam persamaan y2 = 12x maka diperoleh persamaan berikut :
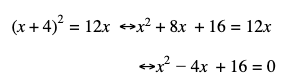
Diskiriman persamaan tersebut adalah :
D = (-4)2 – 4(1)(16)
= 16 – 64
= -48 < 0
Karena D < 0 maka garis y = x + 4 tidak memotong dan tidak menyinggung parabola y2 = 12x.
Contoh soal: penentuan persamaan garis singgung
1. Tentukan persamaan garis singgung pada parabola y2 =4x dari titik P (-1,0).
Pembahasan :
Titik P (-1,0) -> y2 – 4x = 0 ↔ 02 – 4 – 1 = 4 > 0, berarti titik P (-1,0) terletak di luar parabola y2 =4x .
Hasil garis singgungnya adalah
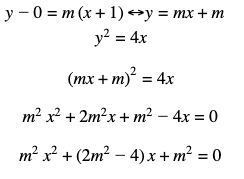
Syarat garis menyinggung parabola adalah D = 0, maka :
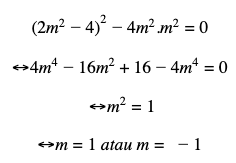
Jadi, persamaan garis singgunya adalah y = x + 1 dan y = – x – 1
Bagaimana Quipperian sudah mulai mengetahui soal pemanasan di atas? Selanjutnya, Quipper Blog akan memberikan soal-soal beserta pembahasannya dari bank soal Quipper. Perlu Quipperian ketahui, bank soal Quipper selalu Up to Date sehingga meyakinkan kamu untuk mempersiapkan setiap ujian yang akan kalian hadapi. Contoh soal tentang Irisan Kerucut pada Parabola adalah sebagai berikut.
Soal: Menentukan Persamaan Parabola dengan titik puncak (0,0)

Pembahasan:

Soal: Menentukan Persamaan Parabola dengan titik puncak (a,b)

Pembahasan :
Soal: Mencari titik fokus pada persamaan parabola
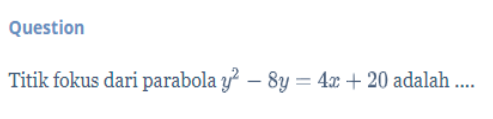
Pembahasan:

Soal: Mencari persamaan parabola yang diketahui puncak dan titik yang melaluinya

Pembahasan:

Soal: Menentukan persamaan garis singgung pada titik puncak (a,b)

Pembahasan:
Soal: menentukan persamaan garis singgung pada puncak (a,b)

Pembahasan :

Bagaimana Quipperian sudah mulai mengenal dan memahami irisan kerucut pada parabola? Ternyata, kalau kita memahami konsep dasar dan dilengkapi dengan latihan soal yang diberikan Quipper Blog, materi matematika tidak sulit ya. Eits, tunggu dulu. Kalau Quipperian ingin lebih memahami konsep pelajaran matematika atau materi pelajaran lainnya. Karena masih banyak video penjelasan konsep materi dari Quipper Super Teacher yang mudah pahami dan menarik pastinya yang akan membuat kamu menguasai setiap pelajaran di sekolah. Ayo bergabung bersama Quipper Video!
Penulis: William Yohanes