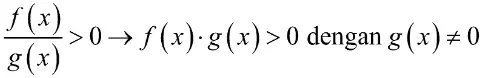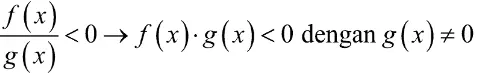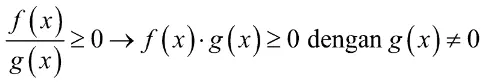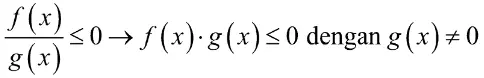Pertidaksamaan Rasional: Pengertian, Sifat, hingga Langkah dan Penerapannya

4.7K

Hai Quipperian, apa kamu sudah pernah belajar tentang pertidaksamaan rasional? Apa yang dimaksud dengan pertidaksamaan rasional? Mudahnya, pertidaksamaan ini memuat suatu fungsi yang disebut fungsi rasional, yaitu f(x) dan g(x). Apa hanya itu?

Daripada penasaran, yuk simak pembahasan tentang pertidaksamaan rasional, sifat-sifat, serta penerapannya berikut ini.

Pengertian Pertidaksamaan Rasional

Pertidaksamaan rasional adalah bentuk pertidaksamaan yang berupa pecahan dengan variabel di bagian pembilang dan penyebut atau penyebutnya saja. Itulah mengapa, pertidaksamaan ini umumnya memuat fungsi rasional f(x) dan g(x). Oleh karena pertidaksamaan, maka akan berlaku tanda “<”, “>”, “≤”, dan “≥” serta garis bilangan. Adapun contoh pertidaksamaan rasional adalah sebagai berikut.

Pertidaksamaan di atas menunjukkan bahwa bagian pembilang dan penyebut sama-sama memuat variabel x. Jika bagian penyebut tidak memuat variabel, maka pertidaksamannya bukan termasuk pertidaksamaan rasional. Contohnya seperti berikut.

→ bukan termasuk percahan rasional

Bentuk Umum Pertidaksamaan Rasional

Bentuk umum pertidaksamaan rasional adalah sebagai berikut.

• atau
• atau

Oleh karena berbentuk pecahan, maka ada syarat yang harus dipenuhi, yaitu penyebut tidak boleh nol atau g(x) ≠ 0.

Sifat-Sifat Pertidaksamaan Rasional

Sifat-sifat pertidaksamaan rasional harus mengacu pada bentuk umum yang telah disebutkan sebelumnya. Adapun sifat-sifatnya adalah sebagai berikut.

• 
• 
• 
• 

Langkah untuk Menyelesaikan Pertidaksamaan Rasional

Untuk memudahkan Quipperian dalam menyelesaikan soal-soal terkait pertidaksamaan rasional, perhatikan langkah-langkah berikut.

1. Jika mengacu pada bentuk umum, ruas kanan pertidaksamaan harus sama dengan nol. Artinya, semua bilangan di ruas kanan harus dipindah ke ruas kiri, sehingga ruas kanannya sama dengan nol.
2. Melakukan pemfaktoran fungsi di bagian pembilang dan penyebut. Langkah ke-2 ini berlaku jika fungsinya berupa fungsi kuadrat atau polinomial derajat lebih dari 1.
3. Menentukan titik pembuat nolnya, baik pada pembilang maupun penyebut.
4. Titik pembuat nol yang diperoleh dari langkah ke-3, digambarkan pada garis bilangan, sehingga kamu akan mendapatkan interval penyelesaian.
5. Menentukan daerah positif atau negatif dengan mensubstitusikan salah satu bilangan di setiap interval ke dalam pertidaksamaan awalnya. Jika substitusi bilangan menghasilkan bilangan positif, berilah tanda (+). Jika substitusi tersebut menghasilkan bilangan negatif, berilah tanda (-).
6. Menentukan daerah penyelesaian dengan menyesuaikan tanda pada interval dengan tanda pertidaksamaan. Misalnya, jika tanda pertidaksamaannya “>0”, kamu harus mencari interval yang tandanya (+). Daerah interval yang tandanya sesuai dengan tanda pertidaksamaan disebut sebagai daerah penyelesaian.

Selain 6 langkah di atas, ada beberapa hal yang perlu kamu perhatikan dalam menentukan tanda pada garis bilangan, yaitu sebagai berikut.

1. Jika tanda pertidaksamaannya “<” atau “>”, maka titik pembuat nol tidak termasuk daerah penyelesaian, sehingga diberi tanda bulatan tidak penuh ( ).
2. Jika tanda pertidaksamaannya “≤” atau “≥”, maka titik pembuat nolnya termasuk daerah penyelesaian (kecuali titik pembuat nol penyebut), sehingga diberi tanda bulatan penuh ( ).
3. Titik pembuat nol pada penyebut tidak boleh masuk daerah penyelesaian karena penyebut tidak boleh bernilai nol.

Perhatikan contoh berikut.

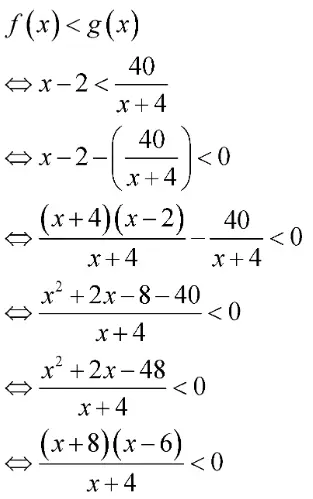
Tentukan pembuat nolnya.

1. Pembuat nol pembilang, x = -8 atau x = 6.
2. Pembuat nol penyebut, x = -4.

Substitusikan nilai x pembuat nol tersebut ke garis bilangan.

Oleh karena tanda pertidaksamaannya “<0”, maka kamu harus mencari daerah penyelesaian yang bertanda (-). Dengan demikian, nilai x yang memenuhi adalah (x<-8) atau (-4<x<6).

Penerapan Pertidaksamaan Rasional

Tidak semua permasalahan matematis bisa diselesaikan dengan sistem persamaan. Ada kalanya, suatu permasalahan hanya bisa diselesaikan dengan sistem pertidaksamaan.

Salah satunya pertidaksamaan rasional. Contoh penerapan pertidaksamaan di dalam kehidupan adalah menentukan estimasi bahan baku suatu perusahaan atau unit produksi, menentukan estimasi jarak antarkota, memperkirakan pertumbuhan suatu tanaman, dan masih banyak lainnya.

Menurut Quipperian, apa lagi contoh penerapan pertidaksamaan ini dalam kehidupan?

Contoh Soal Pertidaksamaan Rasional

Agar pemahamanmu semakin terasah, yuk simak contoh soal berikut.

Contoh Soal 1

Solusi dari pertidaksamaan adalah

1. x >-4
2. x <-3
3. x >-1
4. x <-2
5. x >2

Pembahasan:

Dari pertidaksamaan diperoleh:

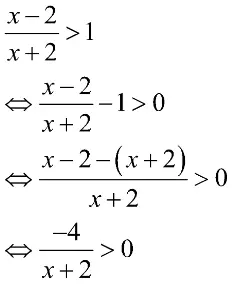
Dari bentuk pertidaksamaan di atas, pembilang = -4 (<0). Agar memenuhi hasil > 0, maka penyebut harus bilangan negatif (< 0), sehingga:

x + 2 < 0

⇔ x < -2

Jadi, solusi dari pertidaksamaan adalah x < -2

Jawaban: D

Contoh Soal 2

Jika x merupakan solusi dari pertidaksamaan nilai x yang memenuhi pertidaksamaan tersebut adalah

1. {-2 < x < -1 atau x > 6}
2. {-4 < x < -1 atau x < 6}
3. {-5 < x < -1 atau x > 5}
4. {-3 < x < 1 atau x > 6}
5. {-2 < x < -1 atau x > 6}

Pembahasan:

Mula-mula, kamu harus mengubah pertidaksamaan tersebut dalam bentuk umumnya.

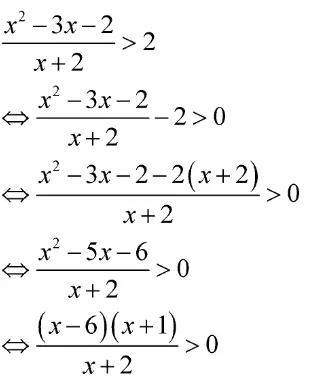
Tentukan pembuat nolnya.

• Pembuat nol pembilang, x = 6 atau x = -1
• Pembuat nol penyebut, x = -2

Substitusi Kan ke garis bilangan

Jadi, nilai x yang memenuhi adalah {-2 < x < -1 atau x > 6}.

Jawaban: E

Contoh Soal 3

Seorang sopir travel mengendarai minibus dari Probolinggo ke Surabaya dengan kecepatan 75 km/jam. Lalu, si sopir kembali pulang dari Surabaya ke Probolinggo dengan kecepatan 50 km/jam. Waktu terlama yang dibutuhkan oleh sopir travel untuk pulang pergi Probolinggo-Surabaya adalah 6 jam. Jarak terjauh antara kedua kota tersebut adalah

1. 150 km
2. 180 km
3. 175 km
4. 200 km
5. 215 km

Pembahasan:

Mula-mula, kamu dapat memisalkan jarak antara Banyuwangi ke Jember sebagai x km.

Dengan demikian;

• lamanya waktu tempuh sopir travel dari Probolinggo ke Surabaya bisa dinyatakan sebagai x/75 jam; dan
• lamanya waktu tempuh sopir travel dari Surabaya ke Probolinggo bisa dinyatakan sebagai x/50 jam

Untuk menentukan jarak terjauhnya, nyatakan kedua permisalan dalam bentuk pertidaksamaan seperti berikut.

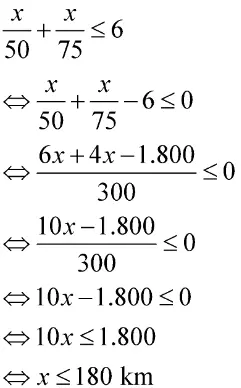
Jadi, jarak paling jauh antara Probolinggo-Surabaya adalah 180 km.

Jawaban: B

Itulah pembahasan Quipper Blog kali ini. Semoga bermanfaat, ya.