Siapa di antara Quipperian yang semasa kecilnya hobi bermain puzzle kayu? Setiap bagian atau kepingan puzzle memiliki bentuk yang berbeda-beda. Nah, kepingan-kepingan tersebut hanya bisa mengisi ruang yang sesuai dengan bentuknya. Hal itu karena bentuk kepingan puzzle kongruen dengan ruang di dalam puzzle. Lalu, apa itu kongruen? Untuk tahu selengkapnya, simak pembahasan berikut.
Pengertian Kongruen
Kongruen adalah kondisi di mana dua bangun atau lebih memiliki bentuk dan ukuran yang sama. Jika bangun satu ditempelkan di atas bangun lain, posisinya tepat dan sesuai. Seperti puzzle yang pernah Quipperian mainkan. Kepingan puzzle akan tepat mengisi ruang yang ukuran dan bentuknya sama.
Kekongruenan
Suatu bangun dikatakan kongruen jika memenuhi syarat-syarat berikut.
- Besarnya sudut yang saling bersesuaian adalah sama.
- Perbandingan semua sisi yang saling bersesuaian bernilai satu karena panjangnya selalu sama.
Perhatikan contoh berikut.
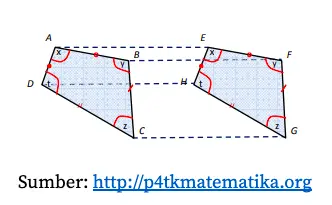
Dari gambar di atas, diperoleh persamaan berikut.
- Besarnya sudut A = sudut E
- Besarnya sudut D = sudut H
- Besarnya sudut B = sudut F
- Besarnya sudut C = sudut G
- Panjang sisi AB = sisi EF
- Panjang sisi CD = GH
- Panjang sisi BC = sisi FG
- Panjang sisi AD = EH
Persamaan di atas menunjukkan bahwa bangun sebelah kiri (bangun ABCD) kongruen dengan bangun sebelah kanan (EFGH). Kekongruenan berlaku untuk semua posisi bangun, misal bangun dirotasi 90o, dirotasi 120o, atau diubah ke posisi lain.
Kekongruenan pada Segitiga
Pada segitiga, kekongruenan bisa ditinjau dari urutan empat besaran, yaitu sisi-sudut-sisi, sudut-sisi-sudut, sisi-sisi-sisi, dan sisi-sudut-sudut. Artinya, Quipperian tidak perlu mengecek persamaan semua sisi dan sudutnya.
1. Kekongruenan sisi-sudut-sisi
Perhatikan bangun segitiga berikut.
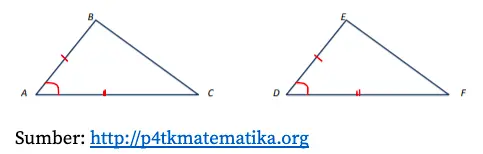
Untuk memastikan kedua segitiga kongruen atau tidak, coba kamu tinjau dari sisi AB terhadap DE, sudut A terhadap D, dan sisi AC terhadap DF. Berikut ini hasilnya.
- Panjang sisi AB = sisi DE karena di kedua sisi terdapat tanda yang sama, yaitu garis merah satu.
- Besarnya sudut A = sudut D karena tanda sudutnya sama.
- Panjang sisi AC = sisi DF karena di kedua sisi terdapat tanda yang sama, yaitu garis merah dua.
Berdasarkan peninjauan sisi-sudut-sisi, diperoleh kesimpulan bahwa segitiga ABC kongruen dengan segitiga DEF (∆ABC ≅ ∆DEF).
2. Kekongruenan sudut-sisi-sudut
Cara kedua untuk menentukan dua segitiga kongruen atau tidak adalah dengan meninjau sudut-sisi-sudut yang saling berdekatan. Perhatikan contoh berikut.
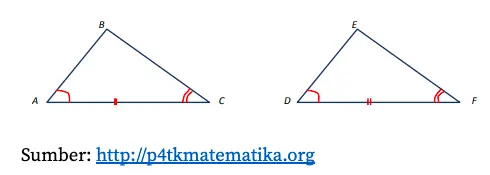
Coba Quipperian perhatikan urutan sudut-sisi-sudut yang bersesuaian! Apakah besar ketiganya sama?
- Besar sudut A = sudut B karena keduanya memiliki tanda yang sama, yaitu garis lengkung merah satu.
- Panjang sisi AC = sisi DF karena kedua garis memiliki tanda yang sama, yaitu garis merah dua.
- Besarnya sudut C = sudut F karena kedua sudut memiliki tanda yang sama, yaitu garis lengkung merah dua.
Berdasarkan tiga persamaan di atas, segitiga ABC kongruen dengan segitiga DEF. Secara matematika, bisa ditulis sebagai ∆ABC ≅ ∆DEF.
3. Kekongruenan sisi-sisi-sisi
Kekongruenan dua segitiga atau lebih juga bisa ditinjau hanya dari tiga sisi yang bersesuaian. Perhatikan gambar berikut.
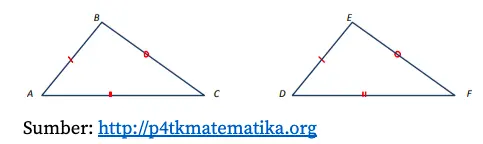
Berdasarkan gambar di atas, diperoleh persamaan berikut.
- Panjang sisi AB = sisi DE karena kedua sisi memiliki tanda yang sama, yaitu garis merah satu.
- Panjang sisi BC = sisi EF karena kedua sisi memiliki tanda yang sama, yaitu lingkaran merah.
- Panjang sisi CA = FD karena kedua sisi memiliki tanda yang sama, yaitu garis merah dua.
Dengan demikian, bisa disimpulkan bahwa segitiga ABC kongruen dengan segitiga DEF atau ∆ABC ≅ ∆DEF.
4. Kekongruenan sisi-sudut-sudut
Dengan melihat sisi-sudut-sudut yang bersesuaian, Quipperian sudah bisa menentukan apakah dua atau lebih segitiga itu kongruen. Perhatikan gambar berikut.
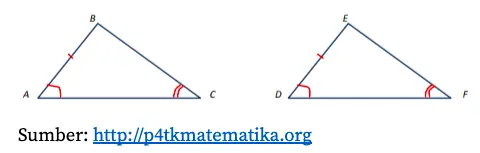
Gambar di atas menunjukkan bahwa besaran sisi-sudut-sudut yang saling bersesuaian adalah sama. Adapun persamaannya adalah sebagai berikut.
- Panjang sisi AB = sisi DF karena kedua sisi memiliki tanda yang sama, yaitu garis merah satu.
- Besarnya sudut A = sudut D karena kedua sudut memiliki tanda yang sama, yaitu garis lengkung merah satu.
- Besarnya sudut C = sudut F karena kedua sudut memiliki tanda yang sama, yaitu garis lengkung merah dua.
Dengan demikian, bisa disimpulkan bahwa segitiga ABC kongruen dengan segitiga DEF atau ∆ABC ≅ ∆DEF.
Apakah Quipperian sudah paham dengan materi kali ini? Agar pemahamanmu semakin meningkat, yuk simak contoh soal berikut ini.
Contoh Soal 1
Perhatikan bangun PQRS berikut.

Bangun tersebut terdiri dari dua segitiga, yaitu segitiga PST dan QSR, yang saling kongruen. Tentukan panjang sisI QT!
Pembahasan:
Pertama, kamu harus menentukan mana saja sisi-sisi yang saling bersesuaian.
Perhatikan segitiga PST!
Panjang sisi PT pada segitiga tersebut belum diketahui nilainya. Oleh sebab itu, Quipperian harus mencari dulu nilainya menggunakan teorema Phytagoras.
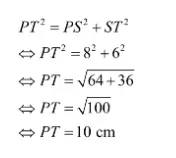
Dari hasil perhitungan diperoleh panjang sisi PT adalah 10 cm. Di soal tertulis bahwa segitiga PST dan QSR kongruen. Dengan demikian, sisi-sisi yang bersesuaian adalah sebagai berikut.
- Panjang sisi PT = QR = 10 cm (sisi miring segitiga)
- Panjang sisi SQ = PS karena SQ = ST + QT, untuk panjang ST saja sudah sama dengan 6 cm.
- Panjang sisi ST = SR (sisi yang paling pendek dari segitiga tersebut).
Oleh karena panjang SQ = PS, maka kamu bisa menentukan panjang sisi QT.
QT = SQ – ST
= 8 – 6
= 2 cm
Jadi, panjang sisi QT adalah 2 cm.
Contoh Soal 2
Perhatikan gambar bangun berikut.

Panjang sisi KL = 5 cm dan panjang sisi OM = 12 cm. Jika segitiga KLM dan NOM kongruen, tentukan keliling bangun di atas!
Pembahasan:
Pertama, kamu harus menentukan sisi-sisi yang bersesuaian seperti berikut.
- Panjang sisi KL = NO = 5 cm
- Panjang sisi LM = OM = 12 cm
- Panjang sisi KM = NM (panjang sisinya bisa kamu cari menggunakan teorema Phytagoras)
Ambil salah satu sisi saja, misal sisi KM.
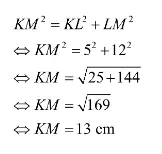
Dengan demikian, panjang sisi KM = NM = 13 cm.
Keliling bangun = KL + LM + MN + NO + OM + KM
= 5 + 12 + 13 + 5 + 12 + 13
= 60 cm
Jadi, keliling bangun tersebut adalah 60 cm.
Itulah pembahasan Quipper Blog kali ini. Semoga bisa bermanfaat buat Quipperian. Jika kamu ingin mendapatkan materi lengkapnya, buruan gabung Quipper Video. Bersama Quipper Video, belajar jadi lebih mudah dan menyenangkan. Salam Quipper!
Penulis: Eka Viandari