Transformasi geometri merupakan sebuah konsep matematika yang dicetuskan matematikawan, Felix Klein. Ia berpendapat bahwa bangun geometri bisa diubah letaknya atau bentuknya, sehingga ada perubahan letak atau bentuk. Ada 4 jenis transformasi geometri: translasi (pergeseran), rotasi (perputaran), refleksi (pencerminan), dan dilatasi (perbesaran/pengecilan atau perkalian.
Halo Quipperian! Kamu pasti pernah dong melihat gedung-gedung tinggi? Atau mungkin rumah-rumah yang minimalis, namun unik dan berjiwa seni yang tinggi? Pernah enggak sih kamu wonder bagaimana gedung-gedung pencakar langit itu bisa berdiri kokoh meskipun diterpa angin?
Kita tentu tahu, seseorang yang membuat dan mendesain bangunan tersebut dikenal dengan nama arsitek. Nah, untuk menjadi seorang arsitek diperlukan bekal ilmu matematika juga lho, yaitu transformasi geometri. Apa itu transformasi geometri? Bagaimana rumusan transformasi geometri tersebut? Penasaran, kan? Yuk, simak jabaran Quipper Blog di bawah ini tentang transformasi geomteri serta persamaan yang dipakai sebagai dasar dalam penentuan letak suatu objek.
Konsep Transformasi Geometri

Konsep transformasi Geometri lahir dari gagasan seorang matematikawan berumur 23 tahun yaitu Felix Klein (1849-1925). Felix Klein mengungkapkan bahwa suatu bangun geometri dapat diubah letaknya atau bentuknya (transformasi), oleh sebab itu ada perubahan letak atau perubahan bentuk dari suatu bangun geometri.
Bangun geometri ini dapat beragam, bisa segitiga, lingkaran, persegi, limas, dan lainnya. Tidak hanya sebuah geometri, garis dan titik pun juga dapat ditransformasikan karena kita tahu bangun ruang adalah kumpulan garis-garis yang dihubungkan secara sistematis, serta garis adalah kumpulan titik-titik yang dihubungkan secara sistematis.
Kenapa Jadi Arsitek Perlu Mengerti Transformasi Geometri?

Untuk menjadi seorang arsitek, diperlukan kemampuan untuk menempatkan suatu objek (bangunan) terhadap titik tertentu dengan akurat dan presisi. Sebagai contoh misalnya arsitek tersebut ingin menempatkan sebuah bangunan tersebut agar tidak terkena sinar matahari.
Apakah bangunan tersebut perlu digeser (translasi)? Berapa meter dari lokasi sebelumnya sehingga tidak terpapar langsung terhadap paparan sinar matahari? Misalnya juga, apakah bangunan tersebut perlu diperkecil (dilatasi) karena ukuran tanah tidak sesuai dengan ukuran tanah yang tersedia? Nah, konsep pergeseran (translasi) atau pengecilan/perbesaran ukuran (dilatasi) dapat kita temui pada pelajaran transformasi geometri. Itulah kenapa kalau kamu mau jadi arsitek, kamu wajib banget menguasai materi yang satu ini.
Jenis-jenis Transformasi Geometri

Ada 4 jenis transformasi geometri yaitu translasi (pergeseran), rotasi (perputaran), refleksi (pencerminan), dan dilatasi (perbesaran/pengecilan atau perkalian). Berikut penjelasannya.
1. Translasi
Translasi (pergeseran) adalah pemindahan suatu objek sepanjang garis lurus dengan arah dan jarak tertentu. Arah dan jarak tertentu itu ditentukan oleh suatu vektor atau ruas garis berarah. Simbol dari suatu vektor adalah adanya tanda panah diatas huruf kapital. Contoh vektor AB ditulis menjadi (→AB).

Dari gambar diatas Quipperian dapat melihat bahwa adanya suatu titik P yang memiliki koordinat (x,y) berwarna biru digeser menjadi P’ (titik merah), lalu digeser lagi kearah P’’ (titik hijau)? Pertanyaanya, bagaimana cara menghitung pergeseran dari titik biru ke titik merah dan titik yang hijau? Rumus translasinya adalah sebagai berikut.

Terlihat dari rumus diatas, bahwa T = ( a b ) adalah pergeseran nilai yang diberikan kepada titik biru sejauh a meter terhadap titik horizontal dan b meter terhadap titik vertikal.
2. Refleksi
Refleksi (pencerminan) adalah transformasi setiap titik pada bangun geometri itu terhadap sebuah garis tertentu yang bertindak sebagai sumbu cermin. Refleksi harus mempunyai sumbu cermin atau acuannya terhadap garis tertentu. Acuannya bisa berbagai macam yaitu pencerminan terhadap sumbu y, pencerminan terhadap sumbu x, pencerminan terhadap garis y = x, pencerminan terhadap garis y = -x, pencerminan terhadap titik O(0,0), dan pencerminan terhadap titik sembarang (y = k). Gambar pencerminan dari titik acuannya dapat dilihat di bawah ini:

Rumus untuk menentukan transformasi refleksi terhadap sumbu X adalah sebagai berikut:

Rumus transformasi refleksi terhadap sumbu Y dapat ditulis sebagai berikut:

Rumus transformasi refleksi terhadap garis y = x dapat ditulis sebagai berikut:

Rumus transformasi refleksi terhadap garis y = -x adalah sebagai berikut:
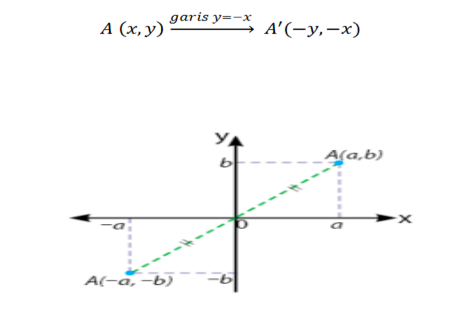
Rumus transformasi refleksi terhadap garis O(0,0) dapat ditulis sebagai berikut:

Transformasi refleksi terhadap garis y = k (k dapat bernilai sembarang) adalah sebagai berikut:

3. Rotasi
Rotasi (perputaran) adalah transformasi dengan proses memutar sembarang titik lain terhadap titik tertentu. Suatu rotasi ditentukan oleh tiga buah unsur yaitu:
- Titik pusat rotasi (apakah acuannya adalah sumbu koordinat O(0,0) atau acuannya titik sembarang P(m,n).
- Besar sudut rotasi menentukan jauhnya rotasi. Ukuran sudut rotasi dapat ditentukan dalam derajat (0), radian (rad), atau bilangan pecahan terhadap satu putaran penuh.
- Arah sudut rotasi. Suatu rotasi dikatakan mempunyai arah positif (+), jika rotasi itu berlawanan dengan arah jarum jam, sedangkan rotasi dikatakan mempunyai arah negatif (-), jika rotasi itu searah dengan arah putaran jarum jam.

Rumus untuk menentukan rotasi dari gambar di atas dapat dinyatakan dalam sebuah matriks sebagai berikut:

Dimana x’ adalah hasil rotasi terhadap titik x, y’ adalah hasil rotasi terhadap titik y, sedangkan x adalah titik awal horizontal dan titik y adalah titik awal vertikal.

Rumus untuk menentukan rotasi terhadap pusat yang sembarang (m,n) adalah sebagai berikut:

4. Dilatasi
Dilatasi (perbesaran/pengecilan atau perkalian) adalah suatu transformasi yang mengubah ukuran (memperbesar atau memperkecil) suatu bangun geometri, tetapi tidak mengubah bentuk bangun geometri itu. Nilai suatu dilatasi ditentukan oleh titik pusat dilatasi dan faktor skalanya (faktor dilatasi). Dilatasi yang berpusat di titik asal O(0,0) dan di titik sebarang P (a,b) dengan masing-masing faktor skala k disimbolkan berturut-turut dengan [O,k] dan [P,k]. Faktor skalanya juga dapat ditulis ke dalam bentuk matriks. Bentuk persamaan transformasi dilatasi adalah sebagai berikut:
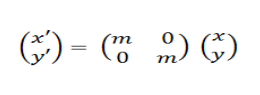
Dilatasi dikatakan diperbesar apabila m > 1 sedangkan dilatasi dikatakan diperkecil apabila m < 1.
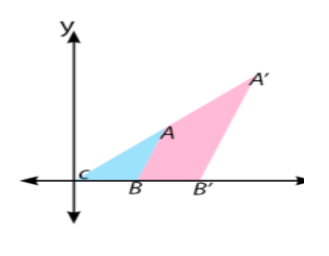
Rumus transformasi dilatasi dengan pusat rotasi O(0,0) adalah sebagai berikut:
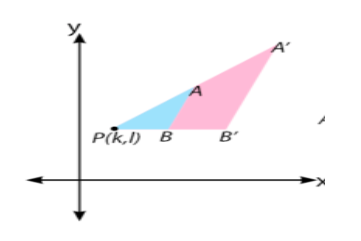
Persamaan transformasi dilatasi dengan pusat rotasi P(k,l) adalah sebagai berikut:
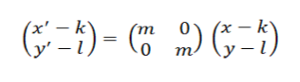
Bagaimana Quipperan sudah mulai tertarik kan untuk belajar tentang transformasi geometri matematika? Agar lebih membantu kamu menguasai konsep transformasi geometri dan menjawab soal-soal transformasi secara mudah dan asyik, kamu bisa gabung bersama Quipper Video. Cusss, langsung subscribe!
Sumber:
- https://en.wikipedia.org/wiki/Felix_Klein
- https://gagasdhio.wordpress.com/2014/06/01/metode-perancangan-arsitektur/
- Tampomas Husein. 2006. Seribu Pena Matematika Jilid 3 untuk SMA/MA kelas XII. Jakarta: Erlangga.
Penulis: William Yohanes